Tensor Operation

In machine learning/big data we can think of a tensor as an nD-array. The picture below is an example of a rank 3 tensor with size (3,4,2).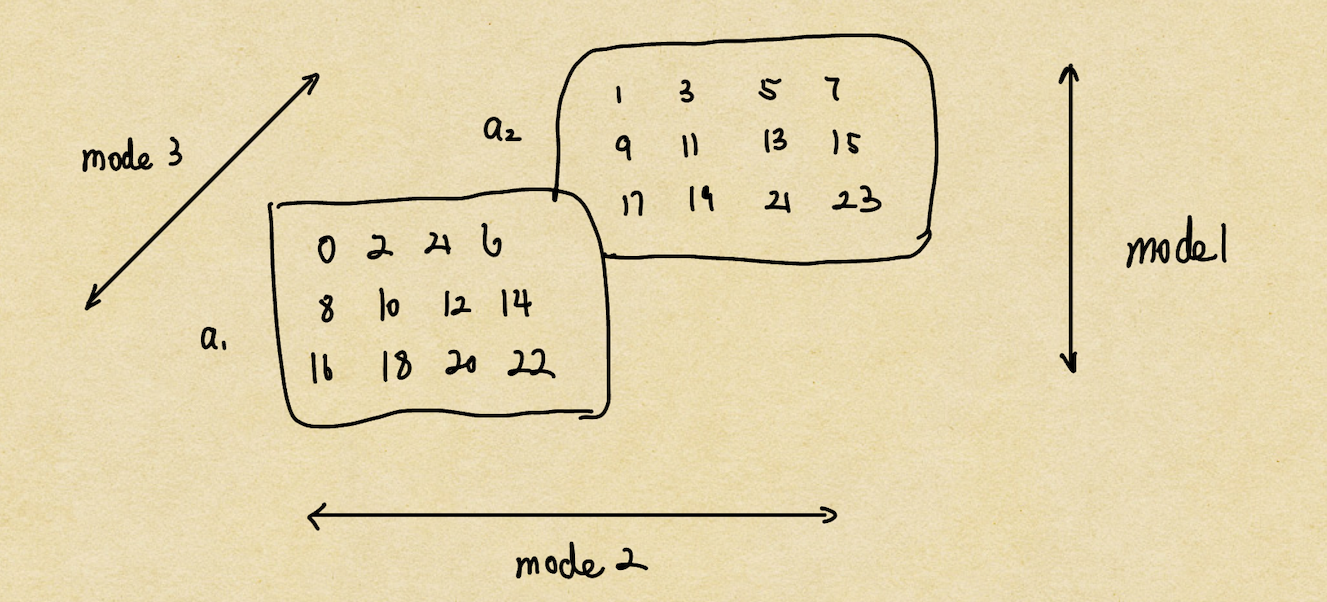

Tensor unfolding

Unfolding a tensor to a matrix (“matrization”) is a
fundamental operation for most tensor methods and we can do it in different ways (use the tensor above as example).

Mode-1 unfolding: The column vectors of $a_n$ are column vectors of $A_1$

$A_{1}=\left(\begin{array}{cccccccc} 0 & 2 & 4 & 6 & 1 & 3 & 5 & 7 \\ 8 & 10 & 12 & 14 & 9 & 11 & 13 & 15 \\ 16 & 18 & 20 & 22 & 17 & 19 & 21 & 23 \end{array}\right)$

Mode-2 unfolding: The row vectors of $a_n$ are column vectors of $A_2$

$A_{2}=\left(\begin{array}{cccccc}0 & 8 & 16 & 1 & 9 & 17 \\ 2 & 10 & 18 & 3 & 11 & 19 \\ 4 & 12 & 20 & 5 & 13 & 21 \\ 6 & 14 & 22 & 7 & 15 & 23\end{array}\right)$

Mode-3 unfolding: The mode-3 vectors of $a_n$ are columns vectors of $A_3$

$A_{3}=\left(\begin{array}{llllllllllll}0 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20 & 22 \\ 1 & 3 & 5 & 7 & 9 & 11 & 13 & 15 & 17 & 19 & 21 & 23\end{array}\right)$

Tensor-matrix multiplication

1-mode multiplication: $U \cdot a_n$ ($U$ is the matrix that we need to multiply, and $a_n$ is the tensor we use)

(1) Mode-1 unfolding the tensor $a_n \rightarrow A_1$

(2) Matrix-matrix multiplication $U \cdot A_{1} = Y_{1}$

(3) Refold (fold the matrix back to a tensor) $Y_{1} \rightarrow y_{1}$

Same principle for mode-2 multiplication and mode-3 multiplication etc.

Outer product

Outer product between two vectors $a^{1}, a^{2}$ is $a^{1} \cdot a^{2^{\top}}$, which is a 2D-matrix of
rank=1 .

Outer product between three vectors $a^{1}, a^{2}, a^{3}$ is a tensor $a_n$ with three slices, and each slice is of rank=1. Each element in the tensor: $a_n(i,j,k)$ is defined by ${a^{1}}_{i} \cdot {a^{2}}_{j} \cdot {a^{3}}_{k}$ ($i$ means i-th slice, $j$ means j-th row, $k$ means k-th column).

Frontal slices: in a $3*3*3$ tensor, the frontal slices is tensor[n, n, n], and n can be :, 0, 1, 2. : means choose all, 0 means to choose the first one, 1 means to choose the second one, and 2 means to choose the third one. The first n represents slice, the second n represents row, and the last n represents column.

# Outer product
import numpy as np
a1 = np.array([1,2,3])
a2 = np.array([4,5,6])
a3 = np.array([7,8,9])
t1 = np.outer(np.outer(a1,a2),a3)
t2 = t1.reshape(3,3,3)
# Frontal slices
t2[:,:,0] # first column of each slice
t2[0,:,:] # first slice