Alpha-Beta Pruning

Alpha-Beta pruning is a search algorithm used to reduce the number of nodes in a minimax search tree. When the algorithm evaluates that the subsequent moves of a strategy are worse than those of the previous strategy, it stops the subsequent development of the strategy. This algorithm achieves the same conclusion as the minimax algorithm, but prunes branches that don't affect the final decision.

Alpha and Beta

\(\alpha\) is the value of the best (highest-value) choice we have found so far at any choice point along the path for MAX. And it's initialized as \(-\infty\).

\(\beta\) the value of the best (lowest-value) choice we have found so far at any choice point along the path for MIN. And it's initialized as \(\infty\).

Example of Pruning

The picture below is a case of a searching tree that has not been cut. In Alpha-Beta pruning, the first layer searches for the largest \(\alpha\), the second layer searches for the smallest \(\beta\), and so on for the following layers. The pruning is performed when the value of a node is larger (or equal) than \(\beta\) of its parent node or smaller (or equal) than \(\alpha\) of its parent node.

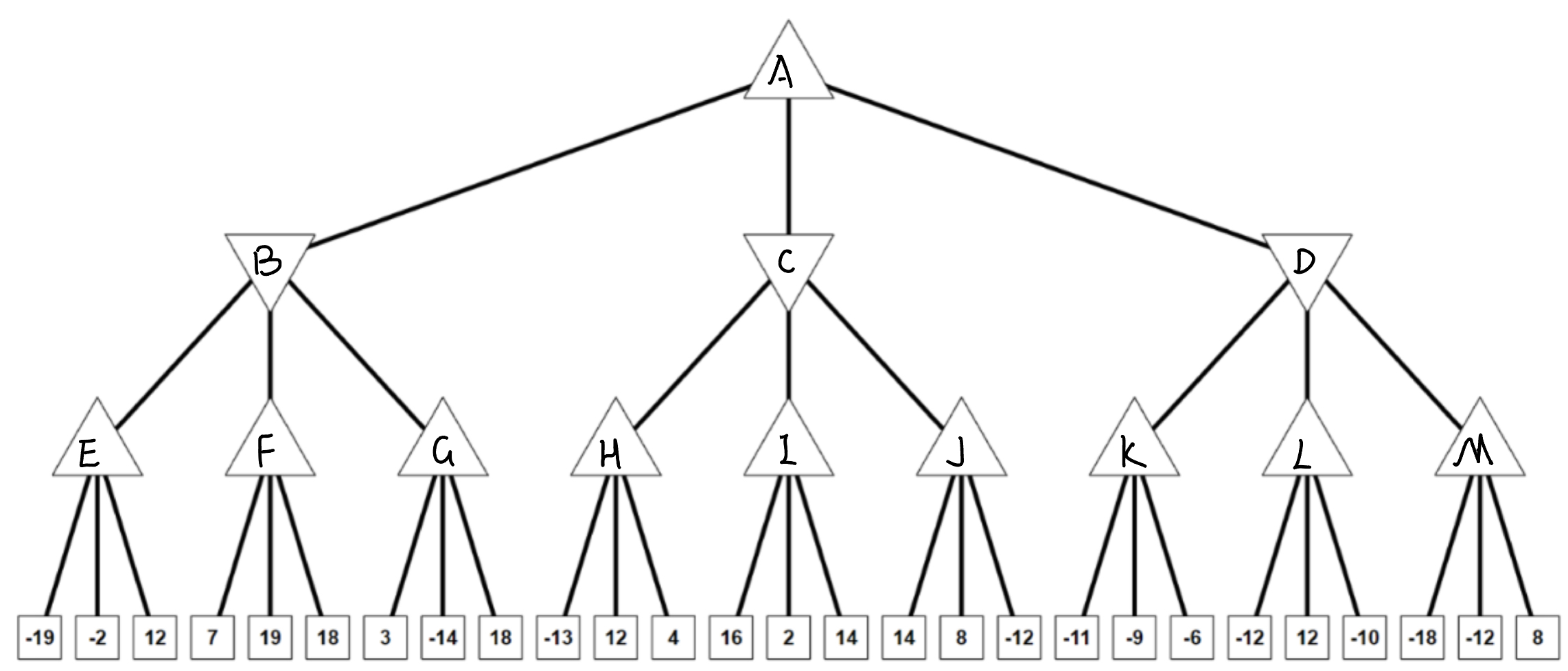
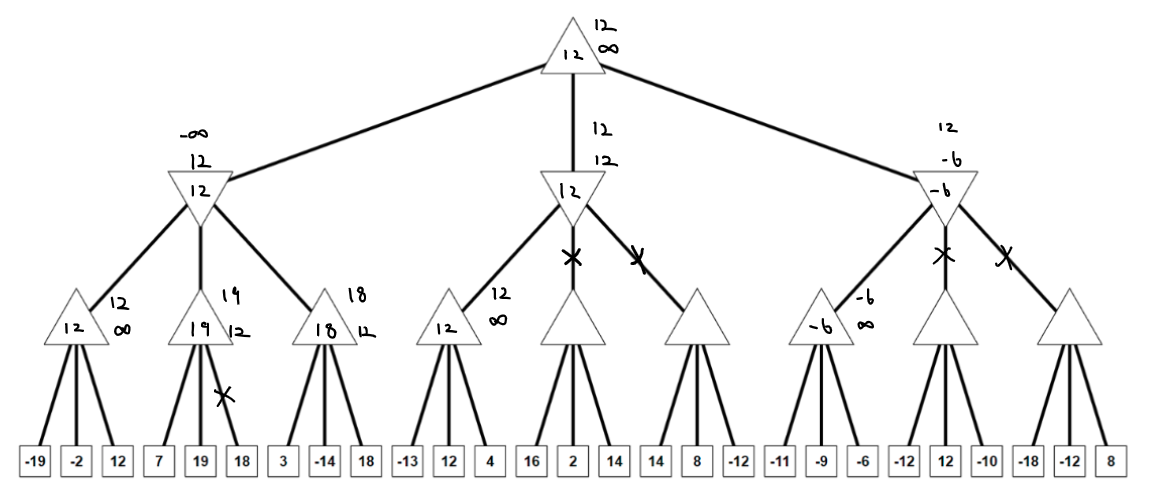
1. Depth-first search starts at A and goes all the way to the last layer (nodes: -19, -2, 12). So the largest one 12 is set as the value for node E, and \(\alpha\) in E is also updated as 12.

2. If the value in a child node is determined, the upper and lower bounds can be returned to the parent node. So \(\beta\) of B can be updated as 12.

3. Keep searching from E to F, the second child node of F is 19, which is larger than \(\beta\) of B. So the searching on this node can stop. So the value of F is set to be 19 and the branch with node 18 is pruned. It's the same for G, its third node is 18, which is larger than \(\beta\) of B, then G is set to be 18.

4. When the child node values of B are all determined, B choose the smallest one (12) to be its value, and its \(\alpha\), \(\beta\) can be returned to its parent node. So \(\alpha\) of A is updated to be 12.

5. Depth-first search starts again from A to child nodes of H. The value of H is set to be its largest child node 12, and its \(\alpha\) is also updated to be 12.

6. The upper bound and lower bound of H is returned to its parent node C. So \(\beta\) of C is updated to be the value of H 12. In this case, \(\beta\) of C is equal with \(\alpha\) of A, so the searching on node C can stop and branches of I and J can be pruned.

7. Then the searching goes from A to the child nodes of K. The value of K and \(\alpha\) of K are both updated to be the largest child node -6.

8. The value of K -6 is returned to node D and it updated to be \(\beta\) of D. Because \(\alpha\) of A is larger than \(\beta\) of D, the searching on node D can stop and branches of L and M can be pruned.

Alpha-Beta Pruning in Python

def max_value(self, node, alpha,beta):
    if(self.isTerminal(node)){
        return node.get_value()
    }
	clf = float('-inf') 
    for chld in node.children:	
        clf = max(clf,min_value(chld, alpha, beta))
        if clf >= beta:
            return clf
        alpha = max(alpha, clf)
    node.val = clf
    return clf

def min_value(self, node, alpha, beta):
    if(self.isTerminal(node)){
        return node.get_value()
    }
	clf = float('inf')
    for chld in node.children:
        chld = min(clf,max_value(chld, alpha, beta))
        if clf <= alpha:
            return clf
        beta = min(beta, clf)
    node.val = clf
    return clf