Breadth-First Search and Depth-First Search

Breadth-First Search (BFS) and Depth-First Search (DFS) are two ways of traversing all vertices in a graph. These two basic search algorithms are introduced below.

Breadth-First Search

• Idea behind BFS

BFS is a traversal strategy for connected graphs, which is similar to the level-order traversal algorithm of binary trees. Its basic idea is: first visit the starting vertex \(v\), then start from \(v\), and visit each unvisited adjacent vertex of \(v\) in turn, \(w_{1} ,w_{2},w_{3}....w_{n}\), and then visit all the unvisited adjacent vertices of \(w_{1} ,w_{2},w_{3}....w_{n}\) in turn, after this, start from these visited vertices, and visit all of their unvisited adjacent vertices. And so on until all vertices on the graph have been visited.

• Algorithm steps for BFS

1. Create an empty array and an empty queue, which are used to determine whether the location has been visited and enqueue unvisited nodes, respectively

2. Add the starting node to queue and set the position of this node on array as 1

3. Pop the first node on the queue out after getting its value, and determine whether the node is the target arrival point

4. If it is the target point, return the result (it usually is the shortest time or the shortest path)

5. If it is not the target point, continue to visit its adjacent nodes, enqueue the adjacent nodes that can be reached, and update the array

6. Repeat step 3, 4, 5 when the queue is not empty

• Example of BFS

The following picture is the search tree of BFS for N-Queen Problem. The number near the node represents the appearance order of each node, \(X\) represents the node that queen would be killed, and the last node is the goal state (it might change for different problem).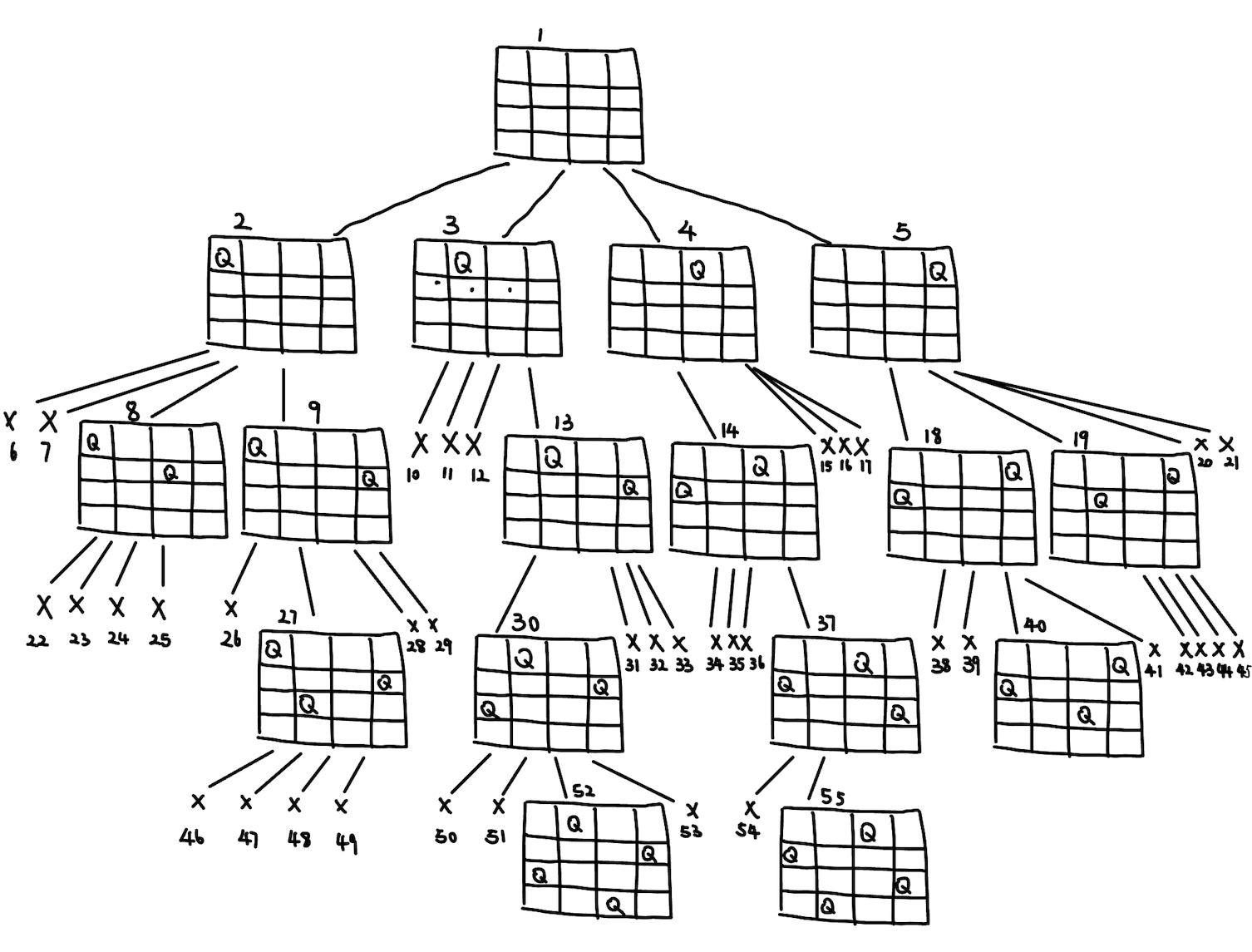

Depth-First Search

• Idea behind DFS

DFS is an algorithm for traversing or searching a tree or graph, which is based on backtracking method. It traverses the nodes of the tree along the depth of the tree, searching for branches of the tree as deep as possible. When the edges of the node \(v\) have been explored or the node does not meet the conditions during the search, the search will backtrack to the starting node of the edge where the node \(v\) is found. The whole process is repeated until all nodes are visited.

• Algorithm steps for DFS

1. Create an empty stack to save unvisited nodes and an empty list to save visited nodes

2. Add the starting node and adjacent nodes stack and list in turn

3. Pop out the last node into the stack and get the node's neighbors from the graph

4. If the adjacent nodes are not on the list, add these nodes to stack and list

5. Output the node that is popped out

6. Repeat the step 3, 4, 5 until the stack is empty

• Example of DFS

The following picture is the search tree of DFS for N-Queen Problem. The number near the node represents the appearance order of each node, \(X\) represents the node that queen would be killed, and the last node is the goal state (it might change for different problem).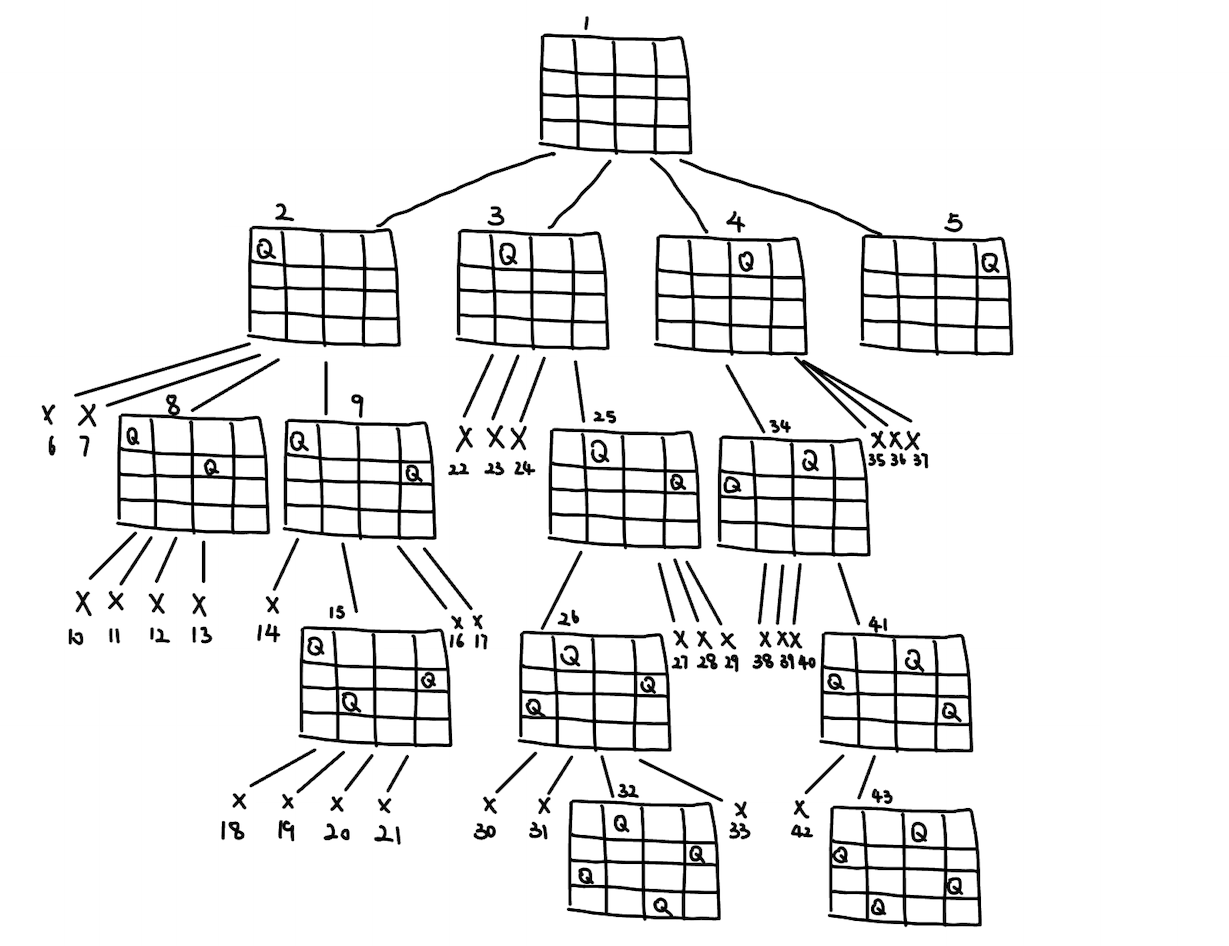

Difference Between BFS and DFS

	BFS	DFS
Access Method	Accessing nodes layer by layer on the graph	Accessing nodes based on depth, visiting a node until reaching its last leaf or no unexplored node on the branch
When to visit next layer	Before visiting the child nodes, all nodes on the same layer has to be explored	Once an unexplored node is found, going the newly found node instead of keeping on exploring the current node
Data Structure	Using queue to store unexplored nodes	Using stack to store unexplored nodes
Characteristic	Slow and require more memory	Fast and need less memory
Application	Finding all connected components in a graph, searching the shortest path between two nodes, finding all nodes within a connected component, testing the biquality of a graph	Topological sorting, searching connected components, solving puzzles like mazes, finding joints (tangent vertices) of graphs

BFS and DFS in Python

class Graph:
    def __init__(self, *args, **kwargs):
        self.neighbors = {}
        self.visited = {}

    def add_nodes(self, nodes):
        for node in nodes: 
            self.add_node(node)
    
    def add_node(self, node):
        print('self.nodes()',self.nodes())
        if node not in self.nodes():
            self.neighbors[node] = [node]

    def add_edge(self, edge):
        u, v = edge
        if u not in self.neighbors[v] and v not in self.neighbors[u]:
            self.neighbors[u].append(v)
            if u != v:  
                self.neighbors[v].append(u)
    
    def nodes(self):
        return self.neighbors.keys()
   
    # DFS with recursion
    def depth_first_search(self, root = None):
        order = []
      
        def dfs(node):
            self.visited[node] = True
            order.append(node)
            for n in self.neighbors[node]:
                if n not in self.visited:
                    dfs(n) 
        if root:
            dfs(root)  # dfs(0)
        # print('visited', self.visited) 
        for node in self.nodes():
            if node not in self.visited:
                dfs(node)
        self.visited = {}
        print(order)
        # print('final visited', self.visited)
        return order
    
    # DFS without recursion
    def depth_first_search_2(self, root=None):
        stack = []
        order = []
        def dfs():
            while stack:
                print('stack',stack)
                node = stack[-1] # 栈顶元素
                for n in self.neighbors[node]:
                    if n not in self.visited:
                        order.append(n)
                        stack.append(n)
                        # stack.append(self.neighbors[n])
                        self.visited[n] = True
                        print('self.visited', self.visited)
                        break
                else: 
                    stack.pop() 
                
        if root:
            stack.append(root)
            order.append(root)
            self.visited[root] = True
            dfs()    
        for node in self.nodes():
            if node not in self.visited:
                stack.append(node)
                order.append(node)
                self.visited[node] = True    
                dfs()       
        # self.visited = {}  
        print(order)
        return order
    
    # BFS
    def breadth_first_search(self,root=None):
        que = []
        order = []
        def bfs():
            while len(que) > 0: 
                node = que.pop(0) 
                self.visited[node] = True
                for n in self.neighbors[node]:
                    print('self.visited', self.visited)
                    print('que', que)
                    if n not in self.visited and n not in que:
                        que.append(n)
                        order.append(n)
        if root:
            que.append(root)
            order.append(root)
            bfs()
            
        for node in self.nodes():
            if not node in self.visited:
                que.append(node)
                order.append(node)
                
        self.visited = {}
        print(order)
        return order